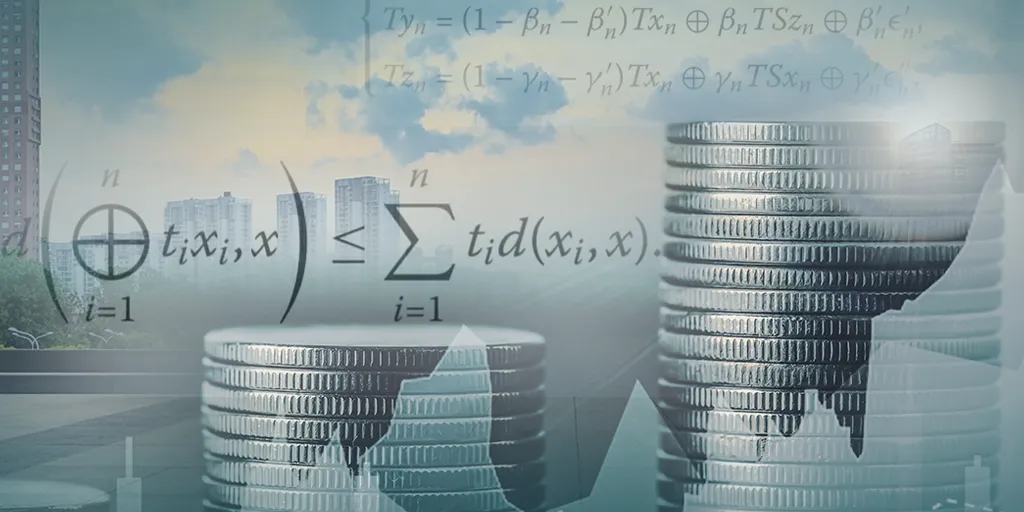Por: Kenyi Calderón Sánchez
Hace ya un par de años, la Universidad de Ciencias Aplicadas y Ambientales U.D.C.A, en un convenio con la Universidad de Jaén (España), ofreció un programa de becas doctorales para profesores, la mayoría, adscritos a la Facultad de Ciencias. Es así, como tuve la fortuna de pertenecer a este selecto grupo de investigadores e iniciar mis estudios de Doctorado en Matemáticas.
Durante la investigación desarrollada en el doctorado tuve la oportunidad de profundizar en un área que, hasta entonces, era desconocida para mí, llamada Teorías métricas del punto fijo, las cuales, estudian la existencia de dichos puntos para operadores definidos en un espacio métrico y bajo condiciones que no son invariantes al pasar a métricas equivalentes.
Una vez finalizado el doctorado, le propuse a la U.D.C.A, un proyecto de investigación con ayuda de pares académicos internacionales, como lo son Juan Martínez, de la Universidad de Jaén y Anantachai Padcharoen, de la Universidad Rajabhat Rambhai Barni (Tailandia), de encontrar teoremas que mostraran convergencia al punto fijo de un operador particular, denominado “T-Ciric quasicontraction”, que ha sido de bastante interés en el mundo académico, por sus grandiosas características y diversas aplicaciones en diferentes campos de la ciencia, entre ellas, en el estudio de modelos de población.
Una vez encontrados los teoremas que nos permitieron afirmar que el algoritmo propuesto converge al punto fijo y además que es único, nos dimos a la tarea de mostrar que dicho algoritmo es estable, desde la definición dada en 1988, por Harder y Hicks. Todo esto está enmarcado en un ambiente métrico de curvatura acotada, que son un caso particular de espacio de longitud y de espacio geodésico.
Finalmente, expusimos cómo los teoremas demostrados durante la investigación pueden ser aplicados a ecuaciones de tipo integral, que cumplen un papel fundamental en las matemáticas, puesto que ellas son las que permiten modelar fenómenos, como la transferencia de energía por radiación, el problema de vibraciones de una cuerda o una membrana, los problemas de viscoelasticidad y algunos problemas de campos electromagnéticos.